Теория графов

Таким образом, матрица инцидентности для ориентированного графа задания имеет вид:

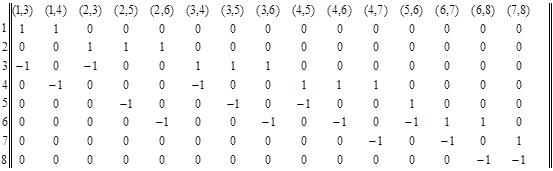
. Упорядочение вершин графа. Алгоритм Фалкерсона

Изменение нумераций узлов и дуг графов, ровно, как и их конфигураций, не изменяет природной сущности явлений и процессов, которые графы описывают. В данной работе - процесс производства молочной продукции. Это свойство графов называется изоморфизмом. Решение задач с привлечением графов упрощается, если вершины и дуги графов расположить в определенном порядке.

Считается, что из пары вершин орграфа вершина i является предшествующей, а вершины j - последующей, если существует путь из i в j, а пути из j в i не существует.

Под упорядочением вершин орграфа понимают такую нумерацию его вершин, при которой:

вершины первой группы не имеют предшествующих, а вершины последней группы - последующих;

вершины любой другой группы не имеют предшествующих, а вершины последней группы - последующих;

вершины одних и тех же групп дугами не соединяются.

После упорядочения вершин получается граф, изоморфный исходному.

Упорядочение вершин орграфа можно осуществить, следуя алгоритму Фалкерсона, включающего в себя следующие шаги:

1. Находят вершины графа, в которые не входят дуги. Это первый уровень вершин. После нумерации они вместе с инцидентными им дугами мысленно удаляются из графа.

2. В оставшемся графе, как и в исходном, находят вершины, в которые не входят дуги. Эти вершины в произвольном порядке нумеруются натуральными числами, следующими после номеров вершин первого уровня. Это вершины второго уровня.

. Выделение уровней и нумерация продолжается вплоть до последней вершины.

Упорядочим нумерацию вершин графа, следуя данному алгоритму:

Рисунок 4.6 - Изоморфный граф

В узел 1 графа задания (рис. 4.2) не входит ни одной дуги, а выходят дуги (1,3), (1,4). Присваиваем узлу 1 номер 1, изображаем этот узел на рис. 4.6 вместе с выходящими из него дугами и мысленно удаляем эту вершину из исходного графа.

Среди оставшихся узлов графа в узел 2 теперь не входит ни одной дуги. Присваиваем узлу номера 2 соответственно и изображаем на рис.4.6. Мысленно удаляем эту вершину вместе с инцидентными ей дугами из графа.

Теперь в узел 3 не входит ни одной дуги. Присваиваем этой вершине номера 3 и переносим ее на рис. 4.6 и мысленно удаляем из графа.

Далее мы видим, что в узел 4 не входит ни одной дуги. Присваиваем ему номер 4 и переносим на новый рисунок, мысленно удалив его из исходного графа.

После проделанной операции остался узел 5 без входящих в него дуг. Присваиваем ему номер 5 и переносим на новый рисунок, мысленно удалив его из исходного графа.

Среди оставшихся узлов графа в узел 6 теперь не входит ни одной дуги. Присваиваем узлу номера 6 соответственно и изображаем на рис.4.6. Мысленно удаляем эту вершину вместе с инцидентными ей дугами из графа.

Теперь в узел 7 не входит ни одной дуги. Присваиваем этой вершине номера 7 , переносим ее на рис. 4.6 и мысленно удаляем из графа.

Остался единственный узел 8 без входящих и выходящих из него дуг. Присваиваем этому узлу номер 8 и изображаем на рис. 4.6.

Таким образом, у нас получился новый упорядоченный граф (рис. 4.6), изоморфный исходному графу (рис. 4.2).

. Максимальная мощность потока.

Алгоритм определения максимального потока:

1. Строится начальный поток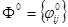

. Выявляются подмножества А вершин, достижимых из истока I по ненасыщенным ребрам. Если при этом сток S не попадет в подмножество А, то построенный поток является максимальным, и задача решена. Если же сток S попадает в подмножество А, то следует перейти к следующему пункту алгоритма.